
데이터마이닝
기업이 보유하고 있는 일일 거래 데이터, 고객 데이터, 상품 데이터 혹은 각종 마케팅 활동에 있어서의 고객 반응 데이터 등과 의외의 외부 데이터를 포함하는 모든 사용가능한 원천 데이터를 기반으로 감춰진 지식, 기대하지 못했던 경향 또는 새로운 규칙 등을 발견하고 이를 실제 비즈니스 의사결정 등에 유용한 정보로 활용하는 일련의 작업
데이터 마이닝 5단계
| 1단계. 목적 정의 | 데이터 마이닝의 명확한 목석 설정 |
| 2단계. 데이터 준비 | 데이터 정제, 데이터 양을 충분히 확보 |
| 3단계. 데이터 가공 | 목적변수를 정의하고 개발환경 구축, 모델링을 위한 데이터 형식으로 가공 |
| 4단계. 데이터 마이닝 기법 적용 | 모델을 목적에 맞게 선택 |
| 5단계. 검증 | 결과에 대한 검증 |
머신 러닝의 알고리즘 종류들
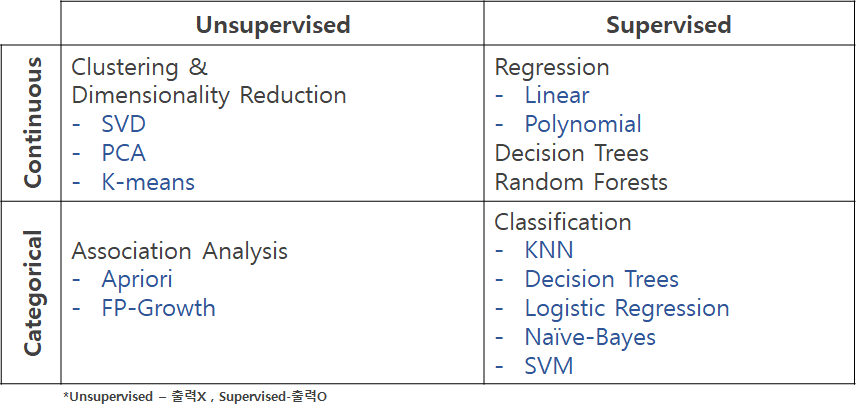
Classification(분류분석)
종류: 로지스틱 회귀, 의사결정 나무, 앙상블, 신경망 모형, KNN, 베이즈 분류 모형, SVM, 유전자 알고리즘
로지스틱 회귀분석
특히 독립변수가 연속형, 종속변수가 범주형일때 적용된다.
ex) 종속변수가 성공/실패, 사망/생존
표현: glm(종속변수~독립변수1+ . . . + 독립변수N, data = df, family=binomial)

| 일반 선형 회귀분석 | 로지스틱 회귀분석 | |
| 종속변수 | 연속형 변수 | 이산형(범주형) 변수 |
| 모형 탐색 방법 | 최소제곱법 | 최대우도법, 가중최소제곱법 |
| 모형 검정 | F-test, T-test | X^2 test |
선형 회귀 분석과 달리 로지스틱 회귀분석은 0~1사이의 값을 가진다. x값에 따른 y값의 변화량을 보는게 목적이 아님!
승산(odds) = 성공률 / 실패율
log odds = log(odds)
sigmoid 함수 : Logistic 함수라고 불리는 log_odds를 연속형 0~1사이 값으로 바꿔주는 함수
의사결정나무(Decison Tree)
의사결정규칙을 나무 규조로 나타내 전체 자료를 몇 개의 소집단으로 분류하거나 예측을 수행
비모수적 모형으로 선형성, 정규성, 등분산성 등의 수학적 가정이 불필요함
범주형과 수치형 변수를 모두 사용 가능
앙상블 모형
여러개의 분류 모형에 의한 결과를 종합하여 분류의 정확도를 높이는 방법
약하게 학습된 여러 모델을 결합해서 사용
과적합 감소 효과가 있다.
상호 연관성이 높으면 분류가 쉽지 않고 정확도가 감소된다.
voting
서로 다른 여러 개의 알고리즘 분류기를 사용해서 결과를 취합해 많은 결과/높은 확률이 나온것을 채택

bagging(Bootstrap AGGregatING)
서로 다른 훈련 데이터 샘플로 훈련, 서로 같은 알고리즘 분류기 결합
여러 모델이 병렬로 학습해서 그 결과를 집계
원데이터에서 중복을 허용하는 크기가 같은 표본을 여러번 단순 임의 복원 추출하여 각 표본에 대해 분류기를 생성
ex) MetaCost Algorithm
boosting
여러 모델이 순차적으로 학습
이상치에 약함, 가중치를 부여하여 표본을 추출
ex) AdaBoost, GradientBoost(XGBoost, Light GBM)
Random forest
배깅에 랜덤 과정을 추가한 방법
노드 내 데이터를 자식 노드로 나누는 기준을 정할 때, 모든 예측 변수에서 최적의 분할을 선택하는 대신, 설명변수의 일부분만을 고려함으로 성능을 높인다.
여러개의 의사결정나무를 사용해, 과적합 문제를 피한다.
KNN(K-Nearest Neighbors)
이웃의 개수(K)만큼 비교해서 결과를 판단하는 방법
K값에 따라 소속되는 그룹이 달라질 수 있다(K값은 hyper parameter) > 사용자가 정해줘야함
스케일링이 중요하고, lazy learning, 지도학습
SVM(Support Vector Machine)
서로 다른 분류에 속한 데이터 간의 간격이 최대가 되는 선을 찾아 이를 기준으로 데이터를 분류
인공신경망(ANN) 모형
인공신경망을 이용하면 분류 및 군집 가능
입력층, 은닉층, 출력층 3개의 층으로 구성되어있다.
학습 : 입력에 대한 올바른 출력이 나오도록 가중치를 조절하는 것
가중치 초기화는 -0.1 ~ 1.0 사이의 임의 값으로 설정하며, 가중치는 지나치게 큰 값으로 초기화하면 활성화 함수를 편향시키게 되며, 활성화 함수가 과적합 되는 상태를 포화상태라고함.
경사하강법 : 함수의 기울기를 낮은쪽으로 계속 이동
제시된 함수의 기울기의 최소값을 찾아내는 머신러닝 알고리즘
인공신경망의 장단점
장점 : 복잡한 비선형관계에 유용하며 이상치/잡음에 민감하지 않음
단점 : 결과에 대한 해석이 쉽지않고 최적 모형 도출이 어렵다. 정규화하지 않으면 지역해(local minimum)에 빠질 위험.
신경망 활성화 함수
풀고자 하는 문제 종류에 따라 활성화 함수의 선택이 달라진다.
| 계단함수 | 0 또는 1 결과 |
| 부호함수 | -1 또는 1 결과 |
| 선형함수 | - |
| sigmoid 함수 | 연속형 0~1, Logistic 함수라 불리기도 함 |
| softmax 함수 | 각범주에 속할 사후 확률을 제공하는 활성화 함수 주로 3개 이상 분류시 사용한다. |

모형평가
| 홀드아웃(Hold Out) | 원천 데이터를 랜덤하게 두 분류로 분리하여 교차검정을 실시하는 방법 잘못된 가설을 가정하게 되는 2종 오류의 발생을 방지 사용법 : idx <- sample(2, nrow ~~ ) |
| 교차검증 (Cross Validation) |
데이터가 충분하지 않을 때 사용. 클래스 불균형 데이터에는 적합하지 않다. 주어진 데이터를 가지고 반복적으로 성과를 측정하여 그 결과를 평균한것으로 모형을 평가 |
| 부트스트랩 (Bootstrap) |
교차검증과 유사하지만, 훈련용 자료를 반복 재선정함 관측치를 한 번 이상 훈련용 자료로 사용하는 복원 추출법에 기반 훈련데이터를 63.2% 사용하는 0.632부트스트랩이 있다. |
오분류표를 활용한 평가지표

F1 : 데이터가 불균형할 때 사용한다.
오분류표 중 정밀도와 재현율의 조화평균을 나타내며 정밀도와 재현율에 같은 가중치를 부여하여 평균한 지표
2 * (Precision * Recall) / (Precision + Recall)
FP rate = 1 - specificity
kappa : 두 평가자의 평가가 얼마나 일치하는지 평가하는 값으로 0~1사이의 값을 가짐
군집분석(Clustering Analysis)
여러 변수 값들로부터 N개의 개체를 유사한 성격을 가지는 몇개의 군집으로 집단화하고 형성된 군집들의 특성을 파악해 군집들 사이의 관계를 분석하는 다변량분석 기법

계층적 군집 분석의 특징
- 가장 유사한 개체를 묶어나가는 식으로 반복해서 군집 형성
- 유사도 판단은 보통 개체간 거리에 기반(유클리드, 맨해튼, 민코프스키, 마할라노비스)
- 이상치에 민감
- 사전에 군집 수 K를 설정할 필요 없다.
- 매 단계에서 지역적 최적화를 수행해 나가는 방법을 사용하므로 그 결과가 전역적인 최적해라고 볼 수 없음
- 한번 군집이 형성되면 군집에 속한 개체는 다른 군집으로 이동할 수 없음
사용법 : hclust(), cluster패키지의 agnes(), mclust()
| 응집형 군집 방법 | 최단 연결법 | 단일 연결법이라고도 하며, 두군집 사이의 거리를 군집에서 하나씩 관측값을 뽑았을 때 나타날 수 있는 최솟값을 측정 |
| 완장 연결법 | 완전 연결법이라고도 하며, 두 군집사이의 거리를 최댓값으로 측정 | |
| 중심 연결법 | 두 군집의 중심간의 거리를 측정 | |
| 와드 연결법 | 계층적 군집내의 오차제곱합에 기초하여 군집을 수행 크기가 비슷한 군집끼리 병합하는 경향이 있다. |
|
| 평균 연결법 | 모든 항목에 대한 거리 평균을 구함, 계산양이 많아질 수 있다. |
수학적 거리 개념 : 유클리드, 맨해튼, 민코프스키
유클리드(Euclidean) > 평소에 구하던 거리 공식
맨해튼(Manhattan) > 두점의 각 성분별 차의 절대값 합
민코프스키(Minkowski) > 거리의 차수와 함께 사용되며, 일반적으로 사용되는 거리 차수는 1,2, 무제한
q=2이면 유클리드, 1이면 맨해튼
통계적 거리 개념 : 표준화, 마할라노비스
표준화 거리 >
References
2021 ADsP 데이터 분석 준전문가, 윤종식 저
https://www.youtube.com/c/EduAtoZPython/videos
EduAtoZ - Programming
An extreme programming education channel
www.youtube.com
'Data analysis > ADsP' 카테고리의 다른 글
| [ADsP][3과목] 4장. 기초 통계 분석 (0) | 2021.08.21 |
|---|---|
| [ADsP][3과목] 4장. 통계분석의 이해 (0) | 2021.08.21 |
| [ADsP][3과목] 3장. 데이터 마트 (0) | 2021.08.20 |
| [ADsP][3과목] 1,2장. 데이터 분석 개요, R프로그래밍 기초 (0) | 2021.08.20 |
| [ADsP][2과목] 2장. 분석 마스터 플랜 (0) | 2021.08.20 |